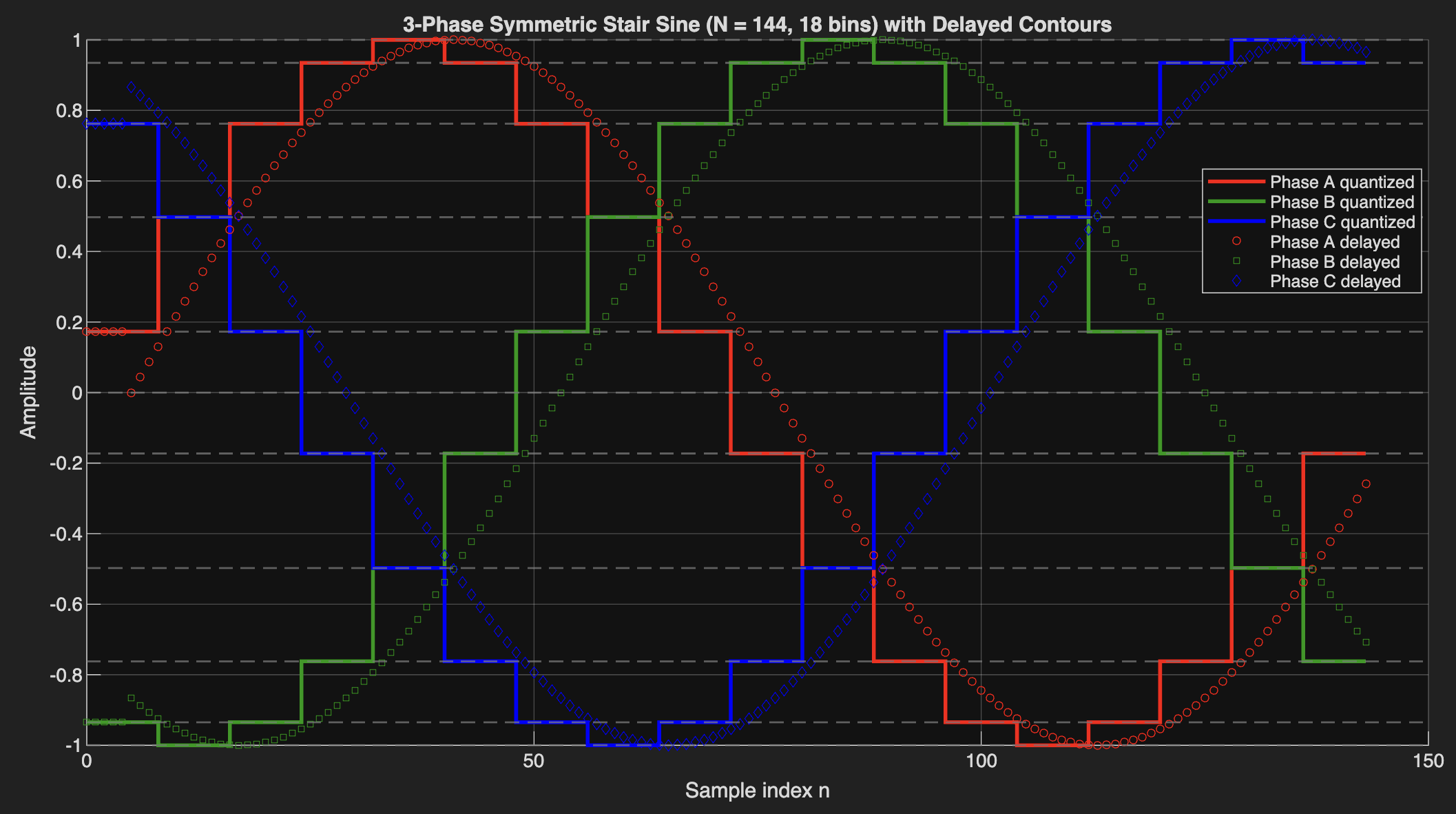
Archive

In many power-electronics and signal-processing applications, we need a quantized staircase approximation of a sine wave—one that remains smooth, symmetric, and perfectly aligned across three phases. This is especially useful when modeling digital PWM systems, lookup-table-based control, or simplified capacitor behavior in rectifiers and inverters.

This post walks through a MATLAB implementation that produces: • A symmetric, smooth staircase sine wave • Three phases shifted by exactly 120° • Perfect stair-edge alignment across all phases • Delayed contour sine waves that mimic a capacitor-like response

Why 18 Bins?

To preserve symmetry (a b c d 1 d c b a …) and still maintain perfect 3-phase timing, both the number of samples per period and the number of bins must be chosen carefully.

Using 144 samples per cycle and 18 bins gives: • 8 samples per bin • 9 bins for the positive half, 9 for the negative half • A 120° shift equal to 6 full bins, which preserves perfectly aligned stair edges

The result is visually smooth and mathematically exact for a 3-phase system.

PS: I used the free online Matlab